一、绘图
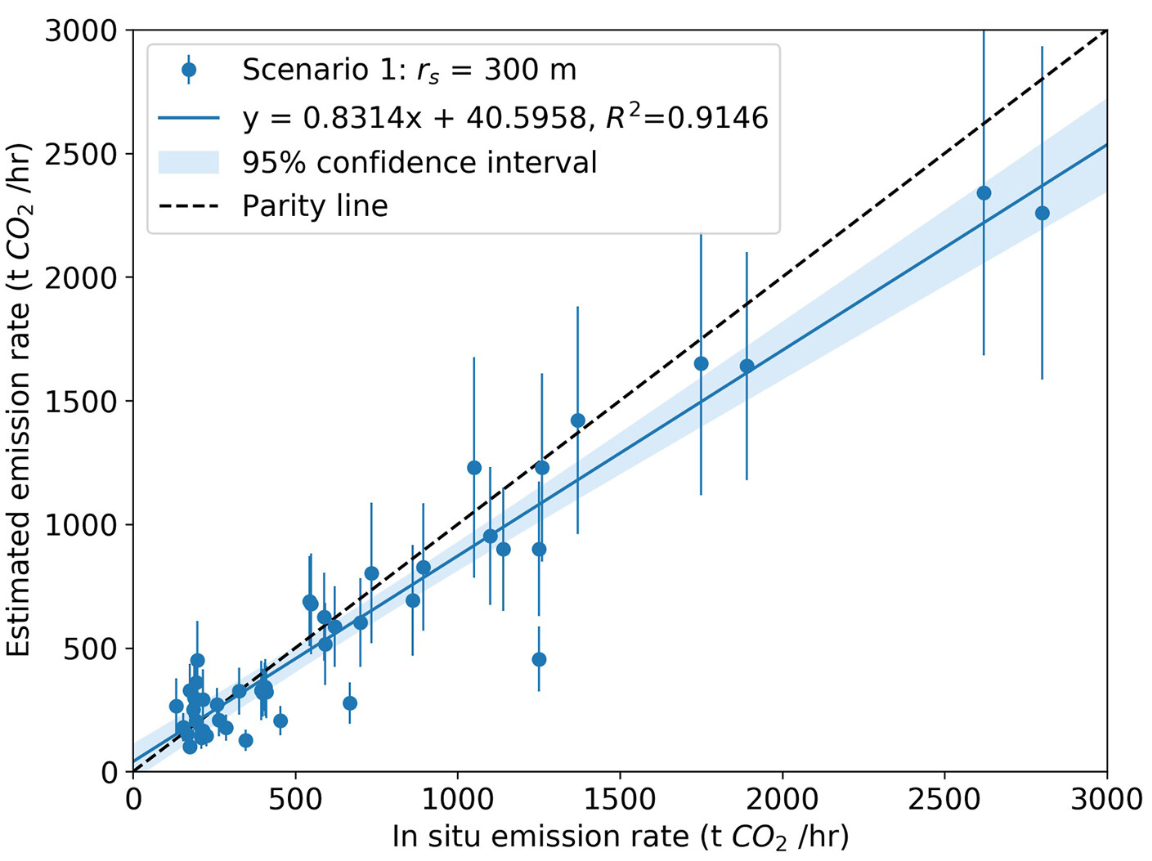
读论文的时候发现一个好看的图(如下),之前知道这种图用R语言来画非常方便,这次想用MATLAB来实现一下。
clc;clear;
x=[1 2 3 4 5 6 7 8 9 10]; % in_situ_emission_rate
y=[11 13 15 14 17 14 18 16 19 20] - 10; % estimated_emission_rate
e = 0.1 * y; % e是误差值,用于绘制误差棒的。这是简单的设置为了 y的0.1倍。
% 给 x 进行排序,方便绘制区间图
[X, I] = sort(x);
Y = y(I);
x = X;
y = Y;
mdl = fitlm(x,y);% 求一元线性拟合的参数,如R2
[p, s] = polyfit(x, y, 1); % 多元线性回归,这里 1 代表是 一元,即 y = kx + b
fprintf("拟合系数分别为:%f %f\n",p(1),p(2));
y1 = polyval(p, x); % fitted line
[yfit, dy] = polyconf(p, x, s, 'predopt', 'curve');
r2 = ['R^2=',num2str(mdl.Rsquared.Ordinary,'%.2f')];% 即一元线性拟合的R平方
fitted_line = ['y=',num2str(p(1),'%.2f'),'x+',num2str(p(2),'%.2f')];
% 开始绘图
figureHandle = figure;
set(gcf,'unit','centimeters','position',[25,15,8.5,8.5]); % 图形窗口在电脑屏幕上的位置和尺寸[左 下 宽 高]
% 单栏图宽度为 8.5 cm,双栏为17.4 mm
p1 = fill([x,fliplr(x)],[yfit-dy,fliplr(yfit+dy)],[217 235 249] / 255, 'FaceA', 0.95, 'EdgeA', 0); % 95% confidence interval
hold on;
p2 = plot(x, y1, 'Color', [20 111 170] / 255, 'linewidth', 1);
hold on;
% p3 = scatter(x, y, 'filled','MarkerFaceColor',[20 111 170] / 255);
p3 = errorbar(x, y, e, 'o','MarkerFaceColor',[20 111 170] / 255,'Color',[20 111 170] / 255); % 使用'o'来表示数据点为圆圈形状
hold on;
p4 = plot(x, x, 'k--','linewidth', 1);
lg = legend([p3,p2,p1,p4],{'N', [fitted_line,', ',r2], '95% confidence interval','Parity line'},'location','NorthWest');
% 坐标区调整
axis tight
set(gca, 'Box', 'off', ... % 边框
'LineWidth', 1,... % 线宽
'XGrid', 'on', 'YGrid', 'on', ... % 网格
'TickDir', 'out', 'TickLength', [.015 .015], ... % 刻度
'XMinorTick', 'off', 'YMinorTick', 'off', ... % 小刻度
'XColor', [.1 .1 .1], 'YColor', [.1 .1 .1]) % 坐标轴颜色
% 坐标轴刻度调整
% set(gca, 'YTick', 0:100:500,...
% 'Ylim' , [-10 510], ...
% 'Xlim' , [-10 510], ...
% 'XTick', 0:100:500)
%'Xticklabel',{'S1' 'S2' 'S3' 'S4' 'S5' 'S6'}
% 字体和字号
set(gca, 'FontName', 'Arial', 'FontSize', 8)
set(lg, 'FontName', 'Arial', 'FontSize', 8)
hXLabel = xlabel('In situ emission rate (t CO_2/hr)');
hYLabel = ylabel('Estimated emission rate (t CO_2/hr)');
set([hXLabel,hYLabel], 'FontName', 'Arial', 'FontSize', 8)
% 背景颜色
set(gcf,'Color',[1 1 1])
% 添加上、右框线
xc = get(gca,'XColor');
yc = get(gca,'YColor');
unit = get(gca,'units');
ax = axes( 'Units', unit,...
'Position',get(gca,'Position'),...
'XAxisLocation','top',...
'YAxisLocation','right',...
'Color','none',...
'XColor',xc,...
'YColor',yc);
set(ax, 'linewidth',1,...
'XTick', [],...
'YTick', []);
%% 图片输出
fileout = 'test';
print(figureHandle,[fileout,'.png'],'-r300','-dpng');
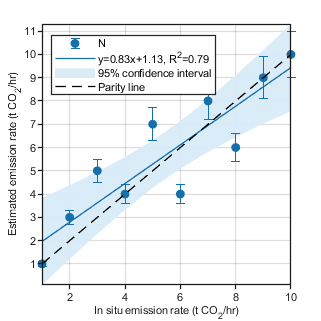
效果如图
二、更深的理解
如果不涉及 95% 置信区间,单纯的线性回归画出最优拟合线,相信大多数人并不陌生。单讲置信区间,也比较容易理解,该博客介绍的很清楚。但如果在线性回归中谈到置信区间,很多人可能就开始懵了。
对于回归方程来说,这里涉及到两个区间
均值的置信区间(confidence interval):
利用估计的回归方程,对于自变量 x 的一个给定值 x0 ,求出因变量 y 的平均值的估计区间。
个体的预测区间(prediction interval):
利用估计的回归方程,对于自变量 x 的一个给定值 x0 ,求出因变量 y 的一个个别值的估计区间。
有点绕是吧,我也看不太懂,来看个具体例子。
不难理解,针对均值的置信区间肯定要窄一些,而具体想预测某一个体值,那区间肯定要宽,因为误差会很大。
比如,让你预测一个高中班级中学生的平均身高,跟让你预测该班级中具体某一个学生的身高,你觉得哪个误差更大呢?对于一个班级的均值,即使你什么信息都不知道,估计预测的也差不到哪儿去,而让你预测班中的张三同学的身高,那你可能就不知所措了。
(1)均值的置信区间
线性回归中,我们假定,对于每一特定的x值,其对应的y值应该是来自一个服从某一均值和标准差的分布。例如,调查温度与手足口发病率的关系,温度=10℃,假定其对应的手足口发病率是来自一个服从均值为10(1/10万),标准差为4(1/10万)的总体分布。
当我们调查这一数据时,得到的是这一总体分布中的某一随机数值(所以说y是随机变量)。根据样本数据建立的回归方程,可以估计出当x等于某一数值时,y的估计值(也就是y的总体均值的估计值)。比如根据方程式:
发病率=-0.011+0.995*温度
可以估计出,温度=10℃时,对应的手足口发病率的均值估计为9.94(1/10万)。
由于是总体均值的估计,那就必然会有估计的误差(标准误),这一标准误是可以计算出来的。
因此根据标准误、均值估计值,便可以估计置信区间。这一置信区间反映的是该范围有多大的信心包含了总体均值。
如月份温度=10℃时,手足口发病率均值的95%置信区间为(6.64,16.25)。这说明,对于温度=10℃这样的月份,我们有95%的信心认为,(6.64,16.25)这一区间包含了手足口发病率的总体均值。其暗含的意思就是(尽管不是很严谨),有95%的信心认为,对于温度=10℃的所有月份,它们对应的手足口发病率的均值在(6.64,16.25)之间。这句话虽然不是很严谨,但其隐含的意思其实就是如此。
(2)个体的预测区间
如果我们已知某一特定的x值,想根据该值预测对应的具体y值,也就是预测某个具体值,这就是对个体的预测。例如,调查了多个地区1-12月的气温和手足口发病率,已知11月的温度=10℃,据此预测某一地区11月手足口发病率是多少。这跟均值的置信区间不同,它不是预测所有地区的11月份的平均发病率,而是预测这一个地区11月的发病率。因此其标准误必然更大,当然也可以计算出来(公式略,格式不好调整,感兴趣的等本书出版后看书)。
由于标准误大了,该区间必然要比均值的置信区间要宽。例如,已知某地11月的温度=10℃,如果要预测这一地区11月份的发病率,其95%置信区间为(-1.55,21.44)。可以发现这一区间远远比均值的置信区间要宽得多。
参考链接
用成像光谱测量液化天然气(LNG)接收站的二氧化碳排放 - Zhang - 2023 - 地球物理研究快报 - Wiley Online Library
Plotting different Confidence Intervals around Fitted Line using R and ggplot2