在统计学中,不确定性的传播(或误差的传播)是变量的不确定性(或误差,更具体地说是随机误差)对基于它们的函数的不确定性的影响。当变量是实验测量值时,由于测量限制(如仪器精度),它们具有不确定性,这种不确定性由于函数中变量的组合而传播。
一个比较简单的例子:使用温度计测量温度,单位为摄氏度,假设测得20度,仪器误差为10%,即测量结果为20 +- 0.2 度。如何用华氏度表示这次测量的不确定性,即为简单的误差传播应用(单变量的误差传播)。
对于多个变量,维基百科中给出了误差传播定律的一般形式。
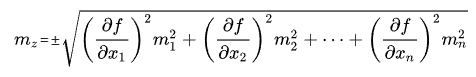
常见的双变量
对于加减法:
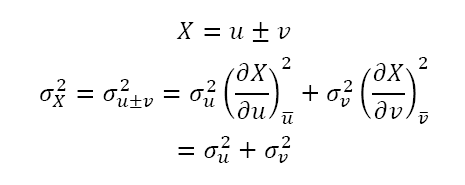
对于乘法:
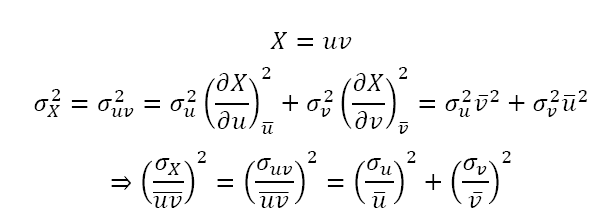
对于除法:
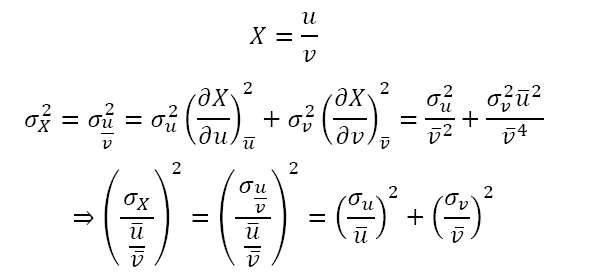
下面是测试代码,可以用来对比传播公式的结果和蒙特卡洛的模拟结果。
clc;clear
N = 1e5;
mean_x = 100;
std_x = 2;
mean_y = 400;
std_y = 80;
x = mean_x + randn(N,1) * std_x;
y = mean_y + randn(N,1) * std_y;
histogram(1./y)
disp(['乘法:蒙特卡洛的结果是',num2str(std(x.*y))])
disp(['乘法:误差传播公式的结果是',num2str( sqrt((mean_x * std_y).^2 + (mean_y * std_x).^2 ) )])
disp(['除法:蒙特卡洛的结果是',num2str( std(x./y) )])
disp(['除法:误差传播公式的结果是',num2str(sqrt( (std_x / mean_y)^2 + std_y^2 * (mean_x/(mean_y^2))^2) )])
histogram(x./y)
值得注意的是,当std_y较小时,除法的两个计算结果是吻合的。但当std_y较大时,除法的两个计算结果相差较大。该现象在乘法中并未出现。究其原因发现,x/y(正态分布除以正态分布)不一定是正态分布。当std_y较小时,分母趋近于一个常数,故最终结果还是正态分布。当std_y较大时,最终结果不再是正态分布,故不是足够大的样本量不足以体现标准差。
三变量
同理,推导出三变量的误差传递公式,并代码测试
%% 三变量
clc;clear
N = 1e7;
mean_x = 100;
std_x = 2;
mean_y = 400;
std_y = 20;
mean_z = 200;
std_z = 2;
x = mean_x + randn(N,1) * std_x;
y = mean_y + randn(N,1) * std_y;
z = mean_z + randn(N,1) * std_z;
histogram(x.*y./z)
disp(['蒙特卡洛的结果是',num2str(std(x.*y./z))])
disp(['误差传播公式的结果是',num2str( sqrt((mean_y / mean_z)^2 * std_x^2 + (mean_x / mean_z)^2 * std_y^2 + (mean_x * mean_y / mean_z^2)^2 * std_z^2 ) )])