今天突然被一个问题给难住，想去搜解决方案但都不知道该怎么描述。具体是这样一个问题：
已知一组向量（2*1）的均值和协方差，想猜测一组向量可能是多少。如果元素间不具有相关性，只存在单个元素各自的方差，那么这个问题就很简单:(normrnd是matlab自带的一个函数，后面的两个参数分别代表$\mu$和$\sigma$)
\[猜测值= \begin{pmatrix} \mu_a\\ \mu_a\\ \end{pmatrix} + \begin{pmatrix} normrnd(0,\sigma_a)\\ normrnd(0,\sigma_b)\\ \end{pmatrix}\]如果单个元素的方差不变，但是两元素间存在相关性时，这个猜测值具体应该等于多少？（这个其实直接百度 “多元相关 random”或者“多元 正态分布” 就可以直接获得答案）。但一开始我甚至都不知道百度什么关键词，于是我便重新认识了一下协方差。
直观理解
首先看一下协方差矩阵的定义是什么？维基百科是这样介绍：“在统计学与概率论中，协方差矩阵（也称离差矩阵、方差-协方差矩阵）是一个矩阵，其 i, j 位置的元素是第 i 个与第 j 个随机变量之间的协方差。这是从标量随机变量到高维度随机向量的自然推广。”
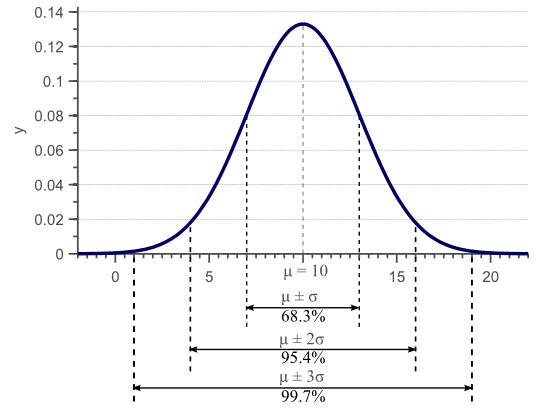
对于标量（表示的是单独的 1 个数）而言，如果样本满足正态分布 $X\sim N(\mu ,\sigma)$，标准差$\sigma$决定了数据分布的幅度，如图1所示。举个例子：假如我在上帝视角下知道一个桌子的真实长度（2米），现在有一把尺子（精度是0.01米），那么一个模拟的测量值就可以表示为10+normrand(0,0.01)。只有当我们做了越来越多次重复测量时，才能尽可能得获得这个桌子的真实长度（多次测量求均值）。如果只进行了一次模拟观测，那么这一次的观测值可以理解为在很多数里面随机挑选了一个出来。
样本方差的无偏估计可由下式获得：
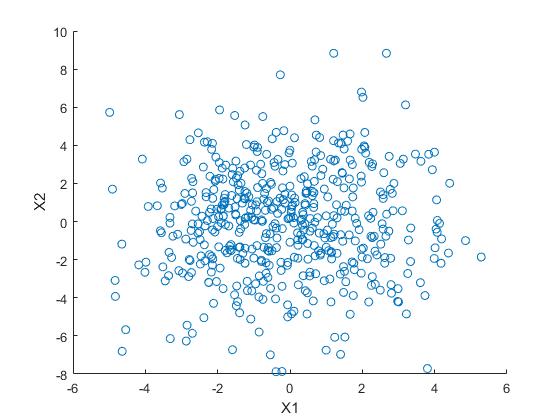
\[\sigma_x = \sigma(x,x) = \frac{1}{N}\ \sum_{i=1}^{N}(x_i - \mu)^2\] 然而，方差只能用于解释平行于特征空间轴方向的数据传播，对于图2所示的二维特征空间，X1和X2不相关。
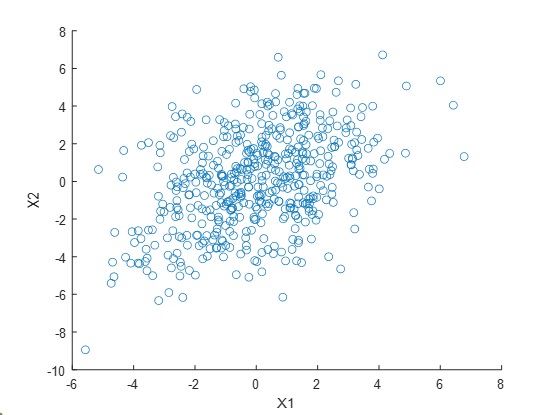
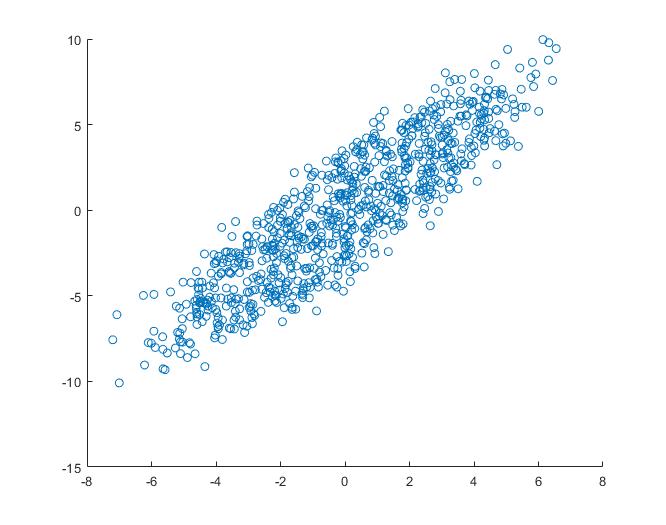
对于下图的二维特征空间，数据存在明显的相关性，即当X1大的时候，X2往往也会比较大。
其对应的概率函数如下图，上图是下图在X1-X2平面的投影
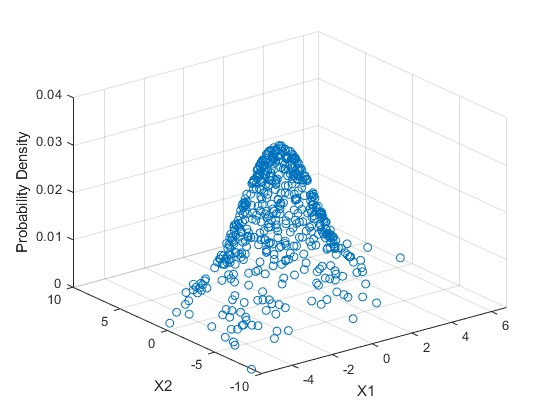对于这组具有相关性的数据，我们仍然可以计算出在X1方向上的方差和X2方向上的方差。然而，数据的水平传播和垂直传播不能解释明显的对角线关系。这种相关性可以通过“协方差”来表达：
\(\Sigma=
\begin{bmatrix}
\sigma(X1,X2) & \sigma(X1,X2)\\
\sigma(X1,X2) & \sigma(X2,X2)\
\end{bmatrix}\)
协方差矩阵始终是一个对称矩阵，其对角线上是方差，非对角线上是协方差。
概率密度
现在已知了均值和协方差矩阵，如果我们可以绘制出图3的那种分布图，模拟一次测量，模拟一次测量值即可以等效为从该图中随机挑选了一个点，这个点的坐标即为测量值。
假设一个向量$X(x_1,x_2,x_3,…,x_k)$满足均值为$\mu$、协方差矩阵为$\Sigma$的多元正态分布，则该分布可以由以下的PDF来描述： \(f(x_1,x_2,x_3,...,x_k) = \frac{e^{-\frac{1}{2}{(x-\mu)}^T \Sigma^{-1} (x-\mu)}} { \sqrt{(\pi)^k \Sigma }}\)
其中$|\Sigma|$表示$\Sigma$的行列式。此处用二元正态分布实例化这个分布，另$X={(x_1,x_2)}^T$，即包含两个随机变量$x_1$和$x_2$。
已知概率密度函数如何生成随机数
常用的两种方法包括 逆分布函数法 (Inverse Transform Method) 和 舍选法 (Acceptance-Rejection Method)参考链接。
这里以舍选法为例做展示。注意这里要是用的随机函数必须是均匀分布（在matlab中要用unifrnd）。
matlab自带的函数
mvnrnd函数可以生成满足某均值以及协方差高斯分布的样本。R = mvnrnd(mu,sigma,n),生成n个样本，这些样本满足均值为mu，协方差为sigma的高斯模型。
本文用到的代码如下：
%%
%多元正态分布
clc;clear
mu = [0 0];
sigma = [4 5;5 8];
X = mvnrnd(mu,sigma,500);
figure1 = figure()
scatter(X(:,1),X(:,2))
xlabel('X1')
ylabel('X2')
y = mvnpdf(X,mu,sigma);
figure2 = figure()
scatter3(X(:,1),X(:,2),y)
xlabel('X1')
ylabel('X2')
zlabel('Probability Density')
%%
%大概算一下概率密度的最大值
m = 0;
for i = 1:10000
x = 100 * rand(2,1);
p = 1 / sqrt(2 * pi * det(sigma)) * exp(-1/2 * (x - mu)' * inv(sigma) * (x - mu));
m = max(p,m);
end
%%
clc;
clear;
mu = [0 0]';
sigma = [4 5;5 8];
%p的最大值 < 0.1
y = 0.1 * unifrnd(0,0.1,50000,1);
index = 1;
for i = 1:50000
x = unifrnd(-30,30,2,1);
p = 1 / sqrt(2 * pi * det(sigma)) * exp(-1/2 * (x - mu)' * inv(sigma) * (x - mu));
if y(i) <= p
fx(:,index) = [x;p];
index = index + 1;
end
end
scatter(fx(1,:),fx(2,:))
参考链接
https://www.datalearner.com/blog/1051485590815771
